Exhaustively solving Scrabble endgames using chess programming techniques
In the summer of 2019, I found myself in Reno, NV competing with 300 other players at the National Scrabble Championship. In the fourth day, I was sitting at a 15-9 record, good enough to play in the top few tables. Actually, I’d been having a pretty good tournament, and just needed to get a win streak going to have a shot at qualifying for the 2-game finals on the fifth day.
In game 25, I faced Alec Sjoholm, a top player from the Pacific Northwest, and he opened with the word SLEAZE for 50 pts. I quickly bingoed with the word ALGUAZIL for 84 pts (an officer of the law in Spain or Latin America), using a blank for the second L, and we were off to the races.
Towards the end of the game, I found myself looking at the following position; my rack is DGILOPR, Alec is holding EGNOQR, and I’m down by 51 points.
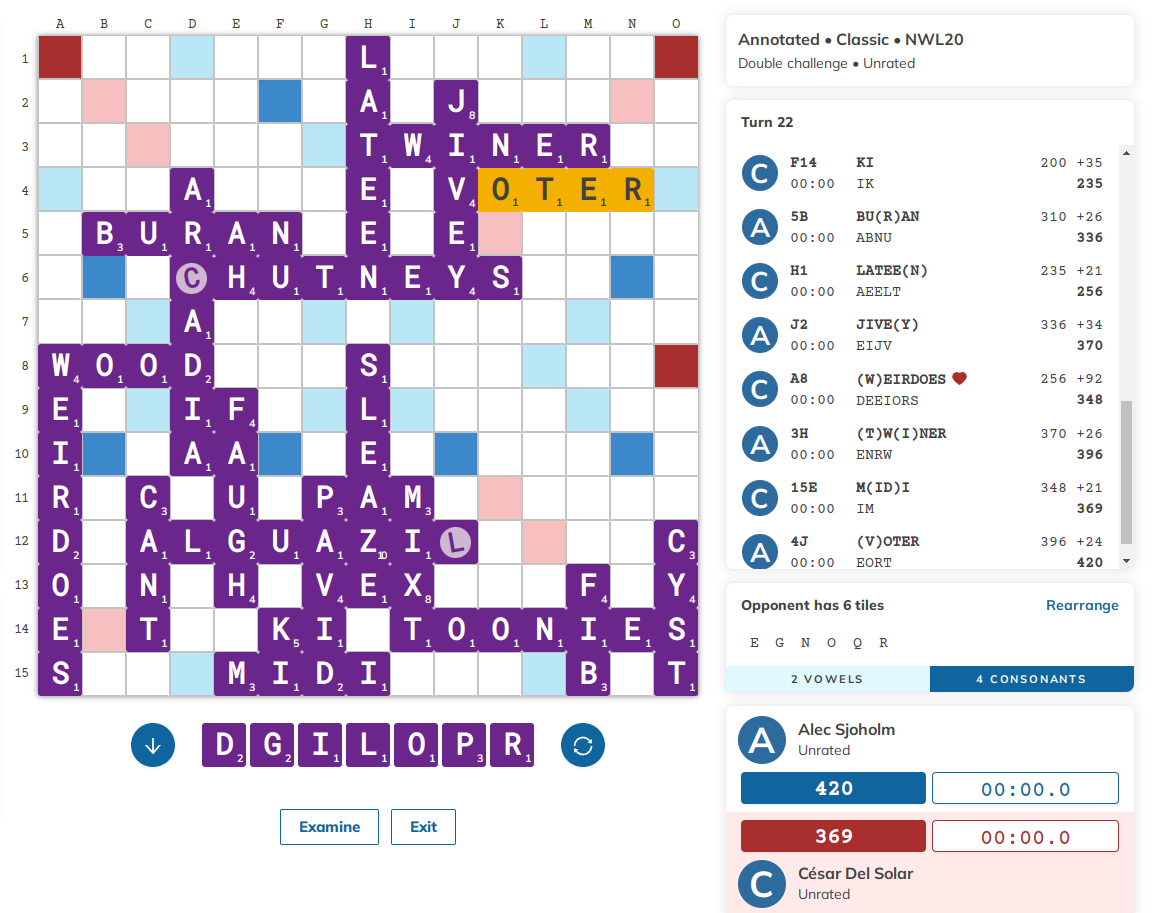
In his commentary for the game, Alec writes that it is one of the most complicated endgames he has ever been involved in. It seems unwinnable from my end, however, my opponent is stuck with the Q. If I am able to play one tile at a time I can get 20 pts at the end of the game for his Q, and I have several minutes to find a way to do it.
Of course, Alec knows this, and he will also try to play one or two tiles at a time to rack up the score on his end. At the end of the game, Scrabble becomes a game of perfect information, and thus we each know the tiles on our opponent’s rack (yes, we track tiles on paper throughout the game).
I played off a single tile, the P, at 7C, for 14 points. In retrospect, this actually turns out to be the beginning of one of the top sequences, although I didn’t know that at the time. My opponent played a small inaccuracy (2J JOG), and I proceeded with an inaccuracy of my own, and so on. After 10 turns or so, the dust was settled and I had lost the game 454-463. It was heartbreaking, particularly because this game all but guaranteed I wasn’t making the finals, but I still ended up finishing 11th overall and won a dictionary for my troubles. Alec went on to win the whole thing the following day.
When I got back home, I was interested to see if I had a possible way to win this game. Quackle, the standard Scrabble analyzer that many of us word freaks use to analyze our games, does not typically look deeply enough for complex endgames. It is still fast and a very formidable analyzer, so this is not meant as a slight on the program. I was not able to get an unambiguous sequence from Quackle, so the question remained open. It was at that point that I resolved to write an endgame solver that can actually give me the answer to this endgame.
Macondo
Macondo is my own generic crossword board game engine; I’ve been working on it for years on and off, and it was meant originally to replicate Quackle, and eventually to use machine learning and other techniques to see if it can be surpassed.
Originally, my plan for the endgame was to use the B* Algorithm that the Maven author (Brian Sheppard) described in his paper. Maven was the first world-class Scrabble engine, and the paper on it was a bit sparse on the B* implementation details. I tried to sketch out a solution, but was unable to understand how B* could possibly do all the evaluation I needed. Additionally, Brian’s in-depth PhD thesis said that B* did fail for some endgames. I wanted to implement something that was sure to find the perfect endgame. I didn’t care about how long it took at the time, I just wanted a solution. I was a man on a mission.
Brian mentioned in his paper that full-width alpha-beta search was the standard way to solve endgames, but with the large branching factor of Scrabble, the big depth to which we must search, and the slower computers of the time, he didn’t think it was possible to do so in a reasonable amount of time. Even now, there are endgames for which a naive minimax algorithm with alpha-beta pruning will still take a fantastic amount of time to solve.
Minimax with alpha-beta pruning
I started implementing minimax with alpha-beta pruning, and after many hours of debugging, I had a working endgame engine by the beginning of 2020. When I plugged this endgame into it, however, my computer would invariably run out of memory. Being new at programming these types of complex algorithms, I was saving way too much state with each node of the tree, and my data structures were all sorts of inefficient. Still, since endgames grow exponentially in complexity as we search deeper, I was still able to manually try a few beginning moves and then the rest of the game would solve in a slightly more reasonable amount of time (read: many hours vs several days).
Evaluation functions
Alpha-beta pruning is heavily reliant on a good “evaluation function”. This function is used to order the moves when doing the search. One of the tricky things about Scrabble endgames is that often the higher scoring move is the best one, so one can just sort by score. But for the complex endgames where people are stuck with tiles, the higher scoring moves are usually the worst moves; it is best to play low-scoring moves instead, or to block your opponent’s high-scoring hotspots. It is difficult to figure out a priori what kind of endgame we are in.
I tried a few complex functions where I determined if a player was stuck with a tile, or if our plays blocked our opponent’s high scoring plays, and assigned various heuristic multipliers to tiles currently on our rack, and tiles that we are stuck with. Many of these functions resulted in modest improvements in search speed, but many also did not. Also, for some endgames, they drastically slowed down the computation. Figuring out if opponents are stuck with a tile, or whether a play blocks another play, is fairly computationally complex, at least when you have to do it all the time while searching the tree.
In the end, a very simple heuristic function probably works best. For every play, Macondo’s current heuristic evaluation function goes like:
- If we are playing off all the tiles on our rack, our estimated value goes up by 2 times the score on our opponent’s rack. This is consistent with Scrabble scoring.
- Otherwise, if we are looking more than 2 plies deep, the estimated value is the score of the play + 3 times the number of played tiles. This still biases us to play more tiles off if we can.
- Otherwise, the estimate is just the score of the play.
Of course, this estimation function is not great for stuck-tile endgames. But those are rarer, and the speed we get from the simplicity of the estimation function makes up for a lot of the increased tree searching. I’m definitely still open to ideas.
When searching down the tree, often an endgame will not end if we’re only searching 1 or 2 plies deep. The value that minimax returns for an un-ended endgame is simply just the score difference between the two players. We are “minimaxing” on this score difference; each player tries to maximize it on their own end. We could have other schemes here, but this works well enough.
Iterative deepening
Iterative deepening is simple: solve the endgame 1 ply deep, then 2 plies deep, then 3 plies deep, and so on. The key is using the move ordering that you get after each previous ply and search the moves the next ply down in that same ordering. Although it seems slow to keep doing the search over and over again, this actually often results in speedups, and it did for us as well.
One of the best things about iterative deepening is that at any point, we can quit searching (for example, if the player is running out of time), and the answer that we get at that point should often be close to correct.
Zobrist hashing
In 2022, a programmer on the Woogles discord added a “killer heuristic” to Macondo. He comes from the chess and shogi programming worlds, so it was great to get input from someone who has experience with other algorithms that I had not looked at. He also helped tune up the evaluation function above.
We first started working on a Zobrist hash together. Is it possible to use Zobrist hashing for Scrabble? It is, and we came up with a decent scheme. Since Scrabble has almost 4 times as many squares as chess, and way more pieces, I believe the probability of collisions would be higher, but with 64 bits, it’s still pretty low.
// A Zobrist hash for crossword board games
type Zobrist struct {
theirTurn uint64
posTable [][]uint64
ourRackTable [][]uint64
theirRackTable [][]uint64
scorelessTurns [3]uint64
boardDim int
}
(See more on Github)
Then, he tried a heuristic where the winner of each minimax call was cached in a dictionary by Zobrist hash. The move would then be tried first every time a position with that same hash was reached. It resulted in a pretty good speedup; coupled with making fixes to not save entire trees in memory, we were able to speed up most complex endgames by around a factor of 2 or more. Still, for complex endgames now the “killer” hash grows and grows in size, so it wasn’t totally ideal.
The reason “killer heuristic” is in quotes is because this is not quite a killer heuristic. When we tried an actual Killer Heuristic – that is, just saving one or two moves that caused a beta-cutoff, indexing these by ply, and searching them first, it never resulted in a speedup, and many times it is actually slower. This might be because the state of Scrabble board might vary drastically between sibling nodes, and the killer heuristic is predicated upon similarity of sibling nodes. We believe that what he actually tried here is more akin to transposition table functionality.
Still, this Alec endgame eluded me. At some point, I believe I was able to find the correct solution by plugging in a few opening moves and leaving it running overnight, but it took many hours, and I still was not sure what the optimal sequence was.
Negamax
One of the downsides of minimax is that any improvements to it have to be done in two branches - the maximizing and the minimizing side. So I took the opportunity a few weeks ago to rewrite it as negamax, which only has a single “branch”. It is essentially the same exact algorithm, but in some ways it is easier to reason about because the valuation of each move is always just from the point of view of the player whose turn it is. But trying to debug negamax with alpha-beta pruning is very tough, at least for me.
Additionally, I rewrote it to just return the value of the node, and not the move itself. This simplifies things a bit and there’s no need to pass around pointers to moves.
Aspiration windows
Sometimes, it may be valuable to know whether an endgame is winnable at all. It can often be a much faster search than to actually find the best win. This can be used if you want to shorten search time; a future pre-endgame engine can also use this to rapidly solve the endgame for the sole purposes of counting it as a win or loss.
In order to do this, we can use an “aspiration window”, where we shorten the initial alpha-beta search window drastically. Setting this window to [-1, 1] based on a setting will result in solutions being clamped to this value. (Note: this works if our negamax is minimaxing on the current score difference between players; you can center the minimal window around other values otherwise). If we can’t find anything better than 0, that’s at best a tie. -1 or worse is a loss. Anything else is a guaranteed win.
Because of the way this works, it will often find solutions that just barely win. This is fine, but an interesting quirk of the algorithm – you better not make any mistakes if you follow this line! Similarly, if it can’t win, it will find slightly wrong sequences that appear to almost win. This is OK - this mode should only be used if we’re quickly trying to find a win.
Aspiration windows can also be used to speed up the algorithm in general by keeping track of whether we fail high or low, and then widening/redoing the search, but I haven’t implemented this yet. The only reason aspiration windows are used in Macondo is to quickly get that binary “is there a win or not” in this endgame.
Principal variation on stack
Since the move is now no longer included in the return value of the negamax call, the principal variation (winning sequence of moves) is harder to build up. I implemented a technique used by the Blunder chess engine to keep track of the principal variation as we iterate through the search function. There are other solutions, such as triangular PV tables, or even just looking up the PV in the transposition table (more below).
Transposition tables
A transposition is basically an identical board position that is reached from two different ways down the tree. For Scrabble, there is a bit more data that is needed – the racks of each player. So a unique position can be described by a board position, both racks, and the player who is currently on turn.
I was originally doubtful about transposition tables, given that Scrabble boards have a lot of volatility. It didn’t seem too likely to me that we’d have many transpositions. But when you have stuck-tile endgames, you will have many situations where you have identical board positions; for example, if you’re playing two moves in two different orders while your opponent is forced to pass their turn, you can save a lot of time not fully searching both of the resultant trees. So I decided to give it a shot.
We had experimented with a simple version of transposition tables above, and I decided to rewrite the algorithm to be more in line with how transposition tables are done for chess. The Negamax Wikipedia page has some great pseudocode for negamax with alpha-beta pruning and transposition tables. I implemented the table as a simple array with a power-of-2 size.
Possible collisions
There are two types of collisions with these type of transposition tables:
- Type-2 collisions, where two positions have different Zobrist hashes, but both hashes have the same value modulo the size of the array.
- Type-1 collisions, where two different positions have the same Zobrist hash.
We can expect type-2 collisions to happen all the time, paradoxically enough. Even with an array size of 2^32, you’re expected to examine roughly 2^16 nodes, or 65K nodes (the square root of the size), before you have a 50% chance of a collision. And some of these endgames go through many millions of nodes. Still, they’re not a big deal – we just replace the node for now. There are other replacement mechanisms we can experiment with.
Type-1 collisions are the real problem, and for now I am ignoring these. 2^64 is quite a big number. One way we can account for them is to store the move with the hash, and verify that it can be played on the board for the value that the table says it has, but that seems like a lot of additional computation.
As a side note, I am often struck by how computationally difficult Scrabble is with relation to chess, in several ways. In chess, it is trivial to store a move with a node; a chess move can be represented by a single 32-bit number. In Scrabble, a move consists of coordinates, the tiles played, and the remaining leave; this is difficult to encode compactly. In chess, the generation of moves is also often fairly trivial. In Scrabble, move generation is by far the biggest component to endgame computation.
What value to store in the table?
Transposition tables at first did not seem to work properly. After a lot of debugging and help from an awesome programming community on Discord, I was able to figure out that the way I had implemented negamax made the current score spread a part of the position. That is, the Zobrist hash needed to have the current spread built into it. This is unideal for several reasons:
- Need a Zobrist or other hashing scheme for the score
- Many more Transposition Table misses - two positions that have the same racks, board positions, and player-on-turn should share a single item on the table, but they didn’t for me.
The solution was to not store the current spread (point difference) in the transposition table, and just add it back in when we pull an item out of the table.
Losing the PV
One downside to transposition tables is that they tend to swallow up your principal variation. For some complex endgames, I only get the first few moves printed out. There’s probably a way to rewrite negamax as negascout/Principal Variation Search, but it’s a matter of how much more complexity we want to add. If we do that though, we can mark PV nodes on the transposition table and then try to avoid replacing them. We can also just play out the first few turns of the game, and use the transposition table to figure out the rest of it.
Luckily, we don’t lose the score of the variation, so we can still be pretty confident it’s correct. I tried it with many different endgames in my tests and manually, and whenever it swallowed up part of the PV, the first few moves were always correct, and the valuation was also correct.
How fast is it?
Transposition tables gave Macondo a huge boost to many complex endgames; I saw as much as a 10-20X speed increase. This is great news!
LazySMP
LazySMP is an optimization used to try to recruit more cores to help solve the endgame. Minimax in general is very hard to parallelize, and I’ve read older papers where people have used hard-to-implement techniques such as dynamic tree splitting. There is a more recent algorithm called “Young Brothers Wait Concept” (YBWC) that was used by many chess programs. Many of these algorithms have similar concepts – categorize the different node types, and apply various heuristics to try to keep all cores as busy as possible.
Lazy SMP is a fairly new optimization that is also simpler to implement. The simplest way to describe it: you’re searching the same endgame multiple times in parallel, sharing the same transposition table, with some slight jitter (some threads can search a ply deeper, they can use slightly different initial orders or start times, etc). For some reason, this actually results in a very good speedup, and Stockfish, one of the most popular chess engines, has switched from YBWC to LazySMP in the last few years.
It only took me a few hours to implement a first version of LazySMP, that roughly works as follows (similar to the pseudocode on the chessprogramming page):
- Create N copies of the game, move generator, and anything else we need.
- Create a move ordering by “solving” down to a single ply with a main core
- For each ply P from 2 to plies: # iterative deepening
- Start N helper threads
- For each thread:
- Solve the endgame down to ply P or ply P+1, depending on whether the thread is even or odd
- Main thread solves the endgame down to ply P
- Stop N helper threads
- Return result from main thread
Note that each helper thread’s job is just to build up the transposition table. The results it returns have no bearing on the result the main thread returns.
With this scheme, I was able to see up to a 3X speedup over straight transposition tables when using 3 threads. After 3 threads, the speedups become much more modest; with 5 or more threads it actually starts slowing down. I’m open to any ideas as to why this is the case and how to utilize the threads more efficiently. My thought is that we’re widening the search tree by too much. I also thought there could be a lot of mutex contention with the transposition table. I turned off mutexes for the table store/load operations and it did give it a little boost in speed, at the cost of possible issues with data integrity (low probability since not only would there have to be a Zobrist type-2 collision, but they’d have to occur at close to the same time). Still, it’s worth investigating using a lockless table scheme.
Conclusions?
There is much I can continue to do with the endgame solver and more ideas I can try. But so far, I am very happy with the results. One of the main things to do next is to use this faster endgame solver to create a perfect pre-endgame solver – a 1-in-the-bag pre-endgame involves solving 8 endgames for each possible pre-endgame play, and then sorting by number of games won. Typically when a person is interested in the result of a pre-endgame, they want to know how many of the pre-endgames result in a win for them. We can apply some optimizations so that the endgame engine stops searching once it has a sure win (or sure loss). Overall, it seems slightly less prohibitive now to build a good pre-endgame solver 😅.
But let’s get back to that Alec game. Did I have a win? No, I didn’t, but the closest sequence is a loss by 3:
- Me: 7C P(A) +14
- Alec: N13 R(E)E +17
- Me: 2J (J)OG +18
- Alec: 7F GO +11
- Me: 9C D(IF) +17
- Alec: 4D (A)N +8
- Me: 6A LI +10
- Alec: (Pass) (stuck with Q)
- Me: 5H (E)R(E) +5
- Me: +20 from his rack = 453 - 456
With LazySMP (using 4 threads) and all the optimizations I talked about above, this endgame solution was found in just 4 and a half minutes. It takes a bit of a deeper search to “prove it correct”, but with prior versions of this, I was not finding the best sequence for many hours, and I wasn’t sure it was even correct because my computer would run out of memory. This is a drastic speedup, made possible by using a lot of techniques from chess programming.
In a way, it is comforting that I didn’t have a win in this endgame. Now I can finally stop thinking about it. 😅
What’s next?
A friend of mine and contributor to the liwords - the source for Woogles - and Macondo codebases is working on a C-based engine that started as a rewrite of Macondo. My goal for this AI is to make it easy for people to analyze their games with it and play with it. Right now it is a command-line based thing that is not super user-friendly. I believe rewriting some of these algorithms in C, and then compiling down to WASM would allow us to embed a fully functional analyzer into the web browser for use with Woogles. Go does not currently play very nicely with WASM.
Woogles has an analyzer that just evaluates plays “statically” - i.e. with score and leave values, but we plan to improve the analyzer to allow Monte Carlo simulations, pre-endgame and endgame solving, inferencing, and other techniques. Stay tuned!